数字孪生常见特效Shader实现3 六边形半球发光护盾

结合上一篇写的光环的光函数，去理解和在创造下面这个在数字孪生中常见的护盾 shield 。

mdb https://www.shadertoy.com/view/sdKXzd	xor https://www.shadertoy.com/view/cltfRf	FabriceNeyret2 https://www.shadertoy.com/view/M32GW3

完整的护盾有以下技术点。

• 六边形 Tile, 在 three.js 中直接通过 geometry 以顶点实现
• uv 映射， 在 three.js 中存储在 geometry 中，本文使用
• 顶点法向量， 用于计算光反射，在 three.js 存储在 geometry 中
• 六边形距离场，这是纯 fragment shader 才会用到
• 边缘菲涅尔光， 本文中将使用极简的方式实现
• 底部光波， 半球与地面交界处发出光，与上节原理一致
• 辉光， 2d 屏幕空间特效，bloom effect， 本文暂不涉及
• 六边形顶点偏移，六边形可以移动 three.js 使用 vertex shader 实现，本文暂不涉及
• 相交高亮， 当一个物体进入护盾，会引发护盾与物体的相交线高亮， 本文暂不涉及
• 自发光， 在六边形与六边形的空隙中，射出光，如下面第二个所示。 本文暂不涉及

# 画六边形

IQ https://www.shadertoy.com/view/Xd2GR3 做六边形 tile 的函数，完全看不懂对吧，因为 IQ 是人形 GPU, 可以直接跳过人类的思维写 GPU 计算最快的代码，而不是人类理解的代码。画一个六边形其实很简单。为了能够让六边形铺满整个平面，需要以下图的方式镶嵌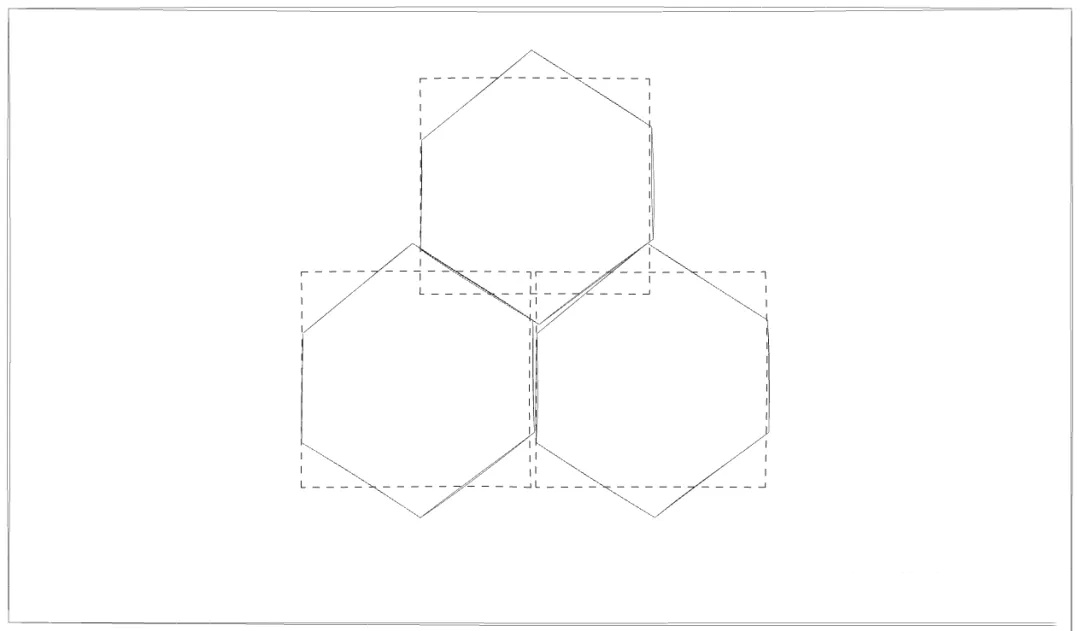

在前面很多文章中有提过制作 grid 的方法，

vec2 gv = fract(uv) - .5;

vec2 gv2 = fract(uv - .5) - .5;

假设我们在 grid 基础上，在做一个 offset (.5) 的 grid 会产生如下的两个 grid.

这个时候我们对两个坐标做一个比较判断

if (length(gv) < length(gv2)) {

    col += vec3(.5);

}

就得到了正方形

不过六边形有一个特点，就是他的高度和宽度是不一样的，高度与宽度比为。也就是说如果我们吧六边形放到正方形中会导致高溢出或者宽度不够，如下图所示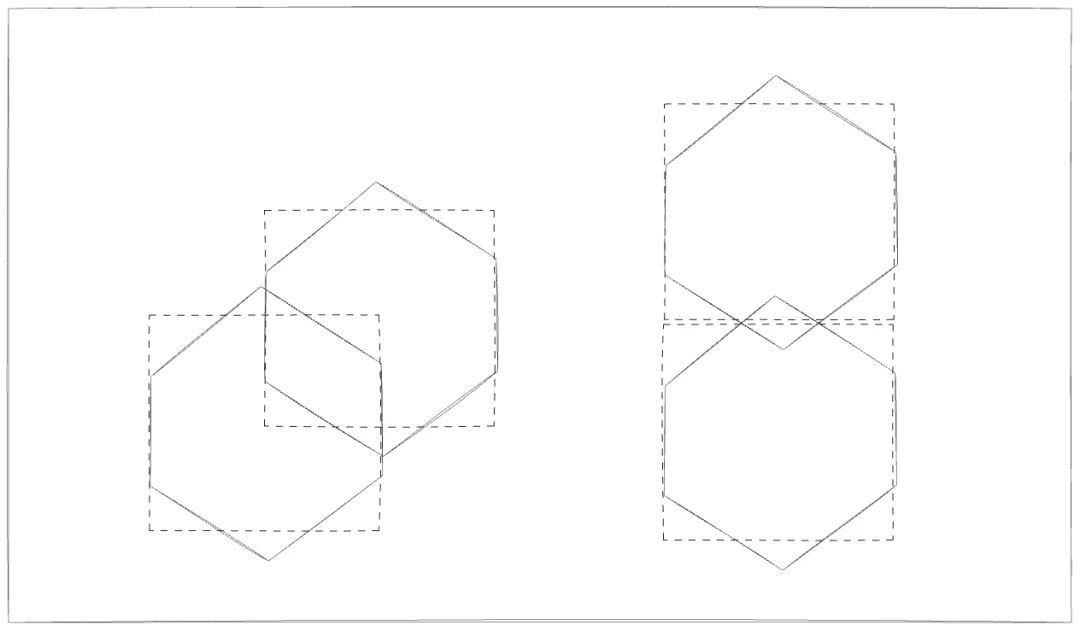

而为了解决溢出的问题，我们的 grid 不能是一个正方形了，grid 应该是一个被拉长的长方形 就像下图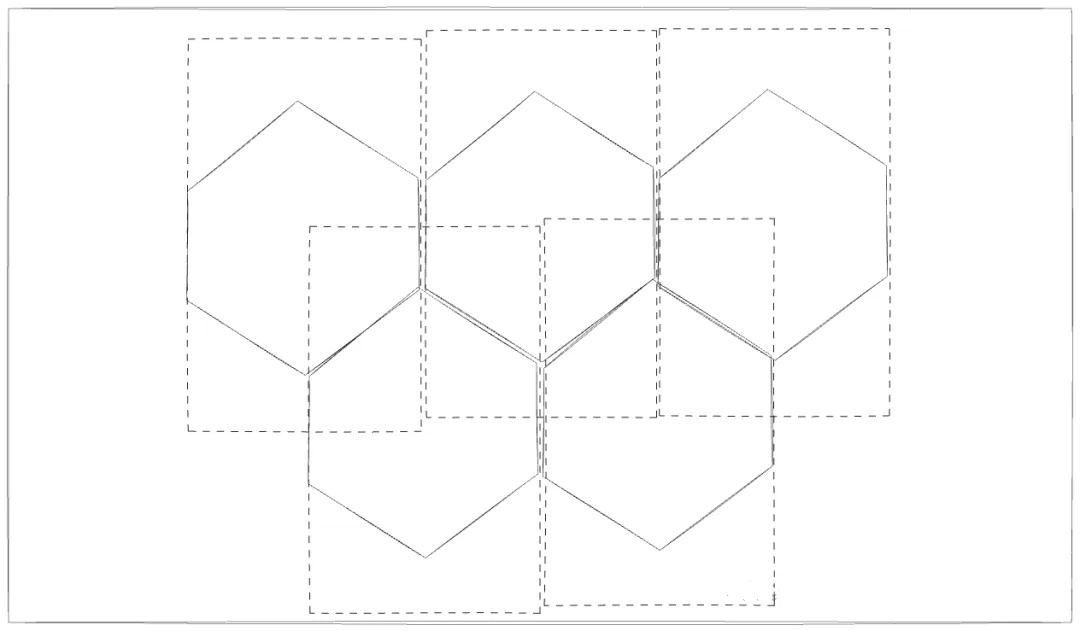

grid 出不同长高非常简单，就是将 fract 函数改为本来的 mod 函数

vec2 r = vec2(1., sqrt(3.));

vec2 h = r * .5;

vec2 a = mod(uv, r) - h;

vec2 b=  mod(uv - h, r) - h;

于是有余下的两个偏移 grid

将分割与颜色补充就可以看到六边形镶嵌了

vec2 gv = length(a) < length(b) ? a : b; col.rg = gv;

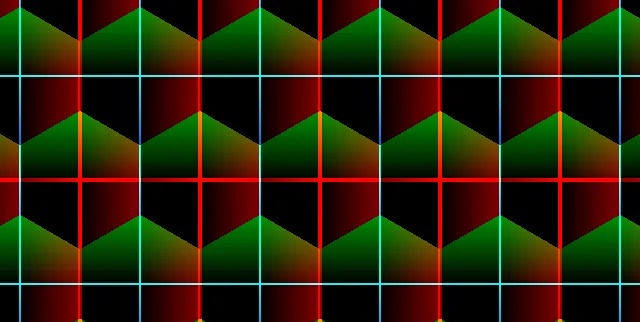
# 六边形距离函数

两个向量的用来表示一个向量在另外一个向量上的投影大小，同时点积的正负号可以表示两个向量的方向。

float d = dot(uv, vec2(1.)); if (d < 0.25 + sin(iTime*3.0) * 0.25) { col.bg = vec2(0.8); } else { col = vec3(0.0); }

下图中的白线表示 vec2 (1.0) 向量的方向，也是 y = x 的函数图像， 可以看出颜色块都是垂直与白线的。

这个时候我们在加上 abs 就可以获得一个正方形了。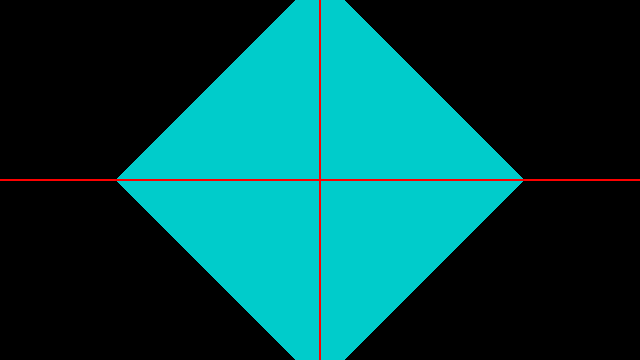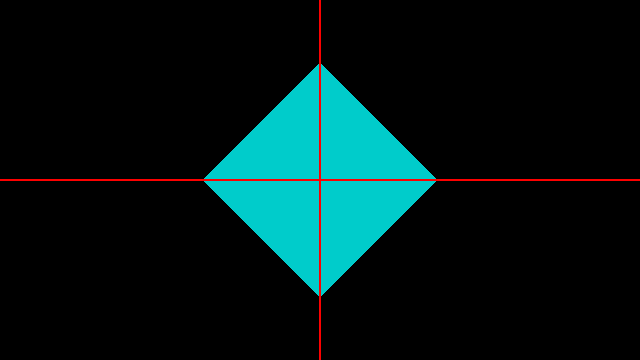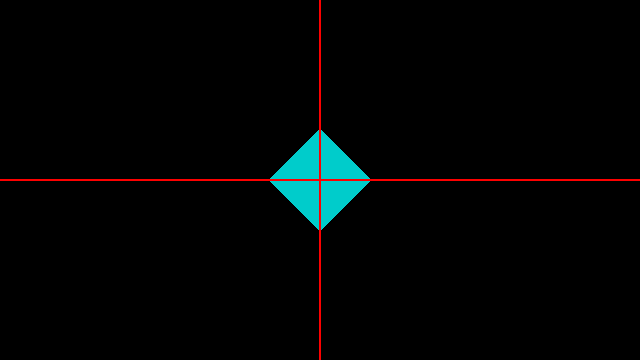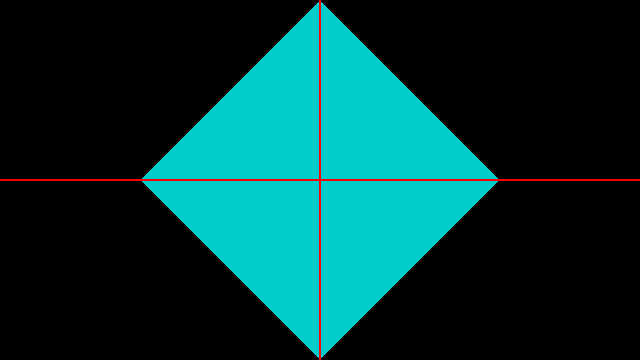

同样的原理如果我们花一个六边形的斜线，只需要找到下图的向量即可。 从图中不难得出向量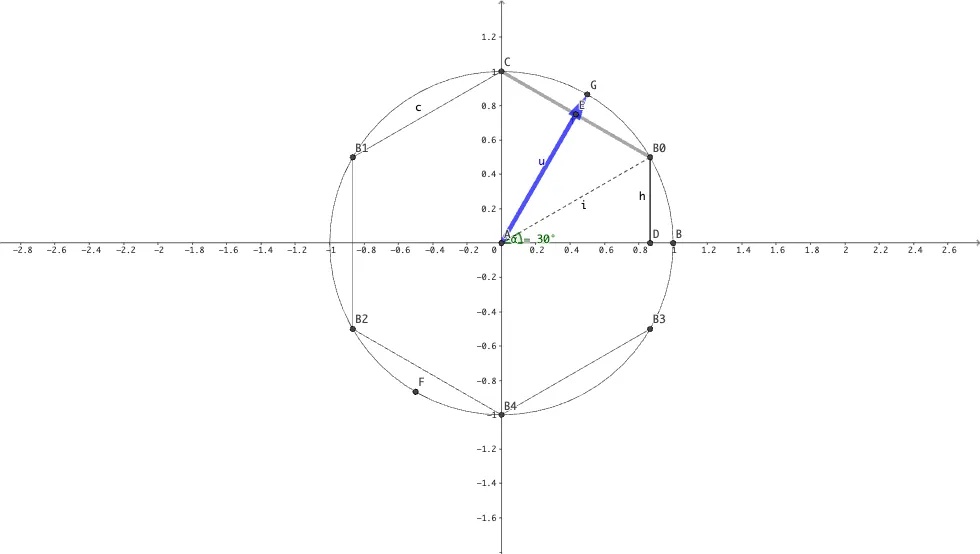修改点积函数

float d = dot(uv, vec2(cos(0.3 * PI), sin(0.3 * PI)));

可以得到菱形

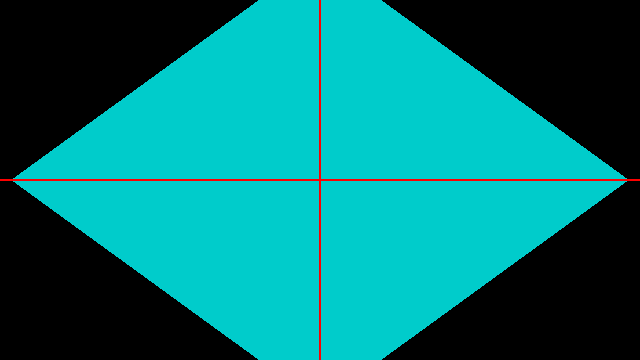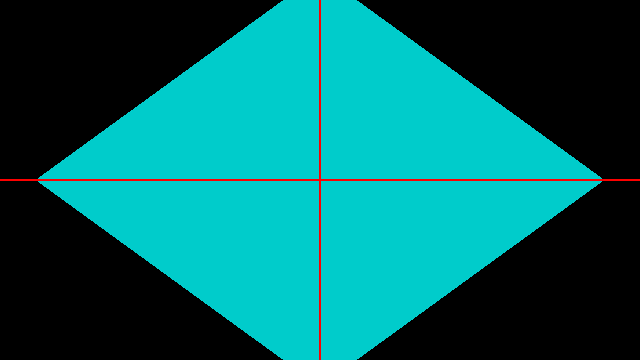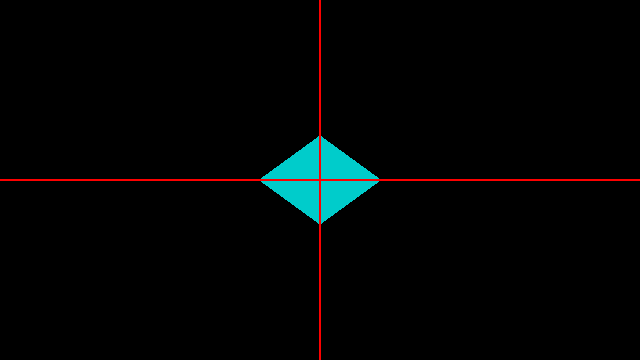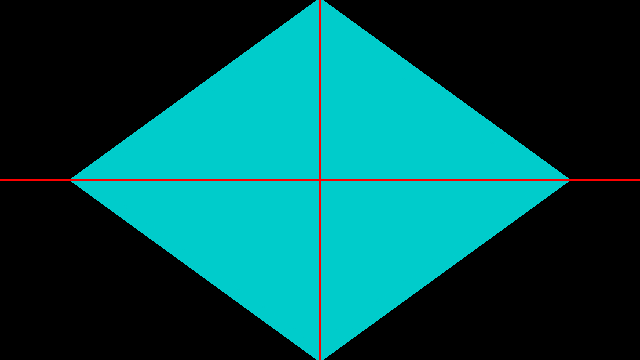
要的到六边形就非常简单点，只需要在 x 轴垂直方向切一刀，

d = max(d, uv.x);

这里面的 d 到底是什么呢？ 其实是沿着六边形边的垂直方向距离 零点的长度，所以其实我们略微修改，就可以变成一个距离边的距离场函数

float SdfHexgon(vec2 p, float r) { p = abs(p); float d = dot(p, vec2(cos(0.3 * PI), sin(0.3 * PI))); d = max(d, p.x); return d - r; } col += step(SdfHexgon(uv, 0.24), 0.0);

于是有

结合上一届的 Tile 函数，我们便可以得到，漂亮的 sdf 六边形镶嵌平面图啦

# UV Mapping

在传统 3d 流水线中，需要线制作 geometry， 然后画纹理，生成纹理贴图。在这里我们有了一个平面的六边形 tile. 想怎么贴就怎么贴... 比如我试验了下面这个隧道，也很漂亮。 他的映射函数为

float a = atan(st.y, st.x);

float r = length(st);

vec2 uv2 = vec2( 0.3/r + 0.2*iTime, a/PI );

更多的映射方法可以参考之前写过的 Shader 3d RayMarching11 常见纹理坐标映射 由于我们做护盾，且实现比较平，所以我们直接采用圆柱映射。同时在角度增加时间，这样可以旋转

float angle = tan(p.x, p.z)/PI;

vec2 uv = mod(vec2(angle+ iTime*0.05, p.y*0.5+0.5), vec2(1.0));

# 球面相交检测

这里计算球面除了需要指导 sdf 之外，还需要知道光线与球面的相交点，这里使用以下代码获取光线与球面相交的两个点

vec2 intersectionWithSphere(vec3 ro, vec3 rd){

 float b = dot(ro, rd);

 float c = dot(ro, ro) - 1.0;

 float delta = b*b - c;

 if(delta < 0.0) return vec2(-1.0);

    return -b + vec2(-1.0, 1.0)*sqrt(delta);

}

这段代码是一个简单的光线相交检测函数，主要用于计算光线与单位球体的交点。下面是对此函数的详细解释：

1. 计算 b 和 c :

   float b = dot(ro, rd); float c = dot(ro, ro) - 1.0;

2. • b 是光线起点 ro 与方向 rd 的点积，表示光线起点与单位球心的投影长度的大小。
   • c 计算的是光线起点到单位球心 (坐标原点) 的距离的平方减去球体的半径的平方（单位球的半径为 1），用于判断光线是否在球体的外部。

3. 计算判别式 delta :

   float delta = b*b - c;

4. • delta 是判别式（决定方程是否有实数根）。这是一个经典的二次方程判别式，决定了光线与球体的相交情况。

5. 判断相交情况:

   if(delta < 0.0) return vec2(-1.0);

6. • 如果 delta 小于 0，表示光线与球体没有交点，函数返回 vec2(-1.0) 表示没有交点的信息。

7. 返回交点:

   return -b + vec2(-1.0, 1.0) * sqrt(delta);

8. • 如果 delta 大于或等于 0，光线与球体有交点。该行代码计算并返回两个可能的交点的距离（相对于光线起点的距离）。
   • -b 是光线起点到交点的距离， sqrt(delta) 是偏移量， vec2(-1.0, 1.0) 表示两个交点（一个是近的交点，一个是远的交点）。

整个函数的作用是通过光线的起点和方向来检测它是否与一个单位球体相交，并返回相交的距离（如果有）。如果光线没有与球相交，则返回 (-1.0, -1.0) 。如果有交点，返回的是到球的两个交点的距离（较近和较远的交点）。

# 基本 3D 空间

关于如何通过 Raymarching，能够纯数学函数构建一个 3D 空间，前面已经积累了大量的文章，有兴趣可以看看，这里我们只为了能够更好看到 sheild 效果，做一个黑色背景与 低颜色地面。另外为边缘增加一点点上一篇文章讲的光环

if(plane < 0.0 && sphere.x < 0.0) {   // background

      return vec3(0.1); 

 }

 if((plane > 0.0 && plane < sphere.x)|| sphere.x < 0.0) {  // ground

     // 底部光环

     float d = 0.02/(abs(length(ro + plane*rd) - 1.0)+0.01);

     vec3 light = vec3(0.690, 0.494, 0.905)*d;

     vec3 ground = vec3(0.115 + 0.05/(plane+1.0));

     return light + ground;

}

# 光的艺术

Fresnel 方程描述了光在不同介质界面上反射和折射时的行为，例如，水面或者眼睛等表面材料在不同的观察方向上会有不同的反射强度。

上图中，远处更多的是看冰山的反射，而近处可以看到水里面的场景， 依照这一个现象也就是在球边缘的位置光越多，而我们直视的位置光越少，越容易穿透。 这里就是使用一个球面法向量与视线的夹角大小做判断即可。 而球的向量最好计算，假设球以世界坐标中心点为球心，那么球面某个点的法向量就是这个点的坐标。 于是有

vec3 p = ro + sphere.x*rd;

vec3 normal = p;

而菲涅尔系数求出来之后，通过 Pow 函数增强，然后赋予颜色

float fresnel = min(1.0 - dot(normal, -rd), 1.0);

fresnel = pow(frs, 3.0)*3.0;

col += vec3(0.690, 0.494, 0.905)*frs;

有点感觉了吧，接下来我们为球与平面的相交处也增加类似于菲涅尔光的效果。只需要一个函数

float frs = max(fresnel, 1.0 - abs((p.y - 0.2)*10.0));

原有为了看距离做的纹理已经不好看了，将其替换成黑色，并且为网格与网格之间增加一些光

col += 7.0*vec3(0.376, 0.333, 0.847)*smoothstep(0.05, 0., ddd)*max(0.1, frs);

col += vec3(0.121, 0.741, 0.615)*smoothstep(0.3, 0., ddd)*max(0.1,0.2);

已经很不错了，但是缺乏立体感。 我们平时在黑板上画球或者正方形，会把视线看不到的背面也做一条辅助线，在这里我们也要使用这种做法，由于我们的球是透光的所以也很合理呀。 视线起来非常简单

if(sphere.y < plane){

    p = ro + sphere.y*rd;

    col += vec3(0.666, 0.996, 0.839)*vec3(0.376, 0.333, 0.847)*pow(max(0.0, 1.0 - abs((p.y - 0.2)*5.0)), 3.0);

}

可以看到上图在看不见的地方也有一个光痕，不过我觉得地面光要在强一点，我们根据里地面的距离远近再来一个地板光增强

if(plane > 0.0){

    float d = 0.2/(abs(length(ro + plane*rd) - 1.0)+0.1);

    col += vec3(0.666, 0.996, 0.839)*vec3(0.690, 0.494, 0.905)*d;

}

终于我们实现了一个半球光护盾

转自公众号：艺术的技术